Tema 5 Introducción a las series de Fourier Elian Alejandro Vazquez.

 En este apartado hablare sobre las series de fourier daré inicio 

5.1 Teoría preliminar

Joseph Fourier nació en 1768 dentro de una familia humilde de Auxerre (Francia) y a la edad de 10 años se quedó huérfano. Eso no le impidió contribuir de forma importante a la egiptología, ostentar altos cargos políticos o escribir el primer texto científico sobre el efecto invernadero, además de convertirse en uno de los matemáticos más célebres de la historia.

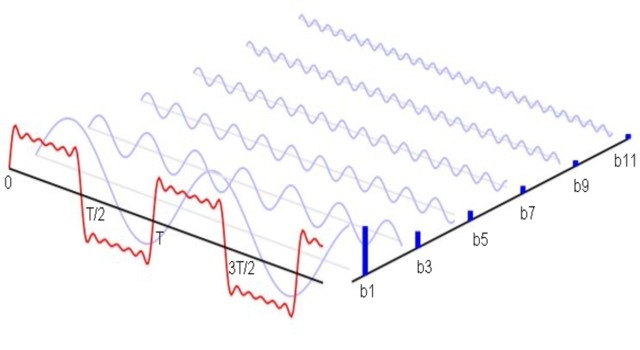
En 1822 publicó la obra Teoría analítica del calor. En ella dedujo una ecuación en derivadas parciales para describir la evolución de la temperatura en un cuerpo sólido y dio un método para resolverla que hoy en día se siguen aprendiendo en las carreras de ciencias e ingenierías. En uno de los pasos de su método, Fourier afirmaba que toda función periódica –que son las funciones que repiten su valor cada cierto intervalo– podía escribirse como una serie de funciones ondulatorias: senos y cosenos. Además, aportó la expresión exacta de los coeficientes de la serie –los valores que multiplican a cada seno y coseno–. Actualmente esta representación se conoce como serie de Fourier de una función. [1]





5.2 Series de Fourier

La Serie de Fourier es una herramienta matemática que nos permite obtener información de una función determinada mediante una transformación (donde entenderemos por “transformación” al proceso que reduce la complejidad de una ecuación



5.3 Series de Fourier en cosenos, senos y de medio intervalo

Desarrollo de f(x) en serie de Fourier de cosenos.-

fp(x)=a02+∑n=1∞ancosnwx  ,  w=πp

an=2p∫p0f(x)cosnwxdx  ,  n=0,1,…

Desarrollo de f(x) en serie de Fourier de senos.-

fi(x)=∑n=1∞bnsennwx  ,  w=πp

bn=2p∫p0f(x)sennwxdx  ,  n=1,2,…

 





Referencias


J. R. MARAVALL, «EL PAIS,» 01 Octubre 2020. [En línea]. Available: https://elpais.com/ciencia/2020-10-01/la-serie-que-cambio-el-mundo.html. [Último acceso: 29 Junio 2022].

c. e. economía, «ELSEVIER,» Octubre 2015. [En línea]. Available: https://www.elsevier.es/es-revista-economia-informa-114-articulo-la-serie-fourier-estimacion-observaciones-S0185084915000389#:~:text=La%20Serie%20de%20Fourier%20es,la%20complejidad%20de%20una%20ecuaci%C3%B3n).. [Último acceso: 29 Junio 2022].

U. d. Cantabria, «Ginematic UC,»  2022. [En línea]. Available: https://www.giematic.unican.es/index.php/series/seriesfourier/sfmediorango. [Último acceso: 29 Junio 2022].




Comentarios

Publicar un comentario

Entradas populares de este blog

Tema 3 Transformada de Laplace Jesus Daniel Ibarra Yepez

Imagen
3.1.1 Definición de la transformada de LAPLACE Las transformadas de Laplace fueron formuladas para transformar una ecuación diferencial que contiene las diferenciales de una función indefinida, a partir de una ecuación t-espaciada hacia una ecuación s-espaciada que puede ser resuelta con mucha facilidad. También pueden ser utilizadas para resolver un sistema de ecuaciones diferenciales. Están dirigidas a una amplia gama de problemas de valor inicial. La transformada de Laplace se denomina a veces transformada operacional; esto es porque transforma las operaciones de integración en simples operaciones algebraicas que son mucho más convenientes de resolver. Después de la cual la aplicación de la técnica de la transformada inversa produce la solución exacta para la ecuación diferencial dada.   3.1.2 Condiciones Suficientes De Existencia Para La Transformada De Laplace Antes de establecer las condiciones para la existencia de la transformada de Laplace   es...
Leer más

Índice Ecuaciones Diferenciales

 Tema 3 Transformada de Laplace. 3.1 Teoría preliminar.   3.1.1 Definición de la transformada de Laplace. Propiedades.   3.1.2 Condiciones suficientes de existencia para la transformada de una función.  3.2 Transformada directa.  3.3 Transformada inversa.  3.4 Función escalón unitario.  3.5 Teoremas de traslación.  3.6 Transformada de funciones multiplicadas por t n, y divididas entre t.  3.7 Transformada de una derivada y derivada de una transformada.  3.8 Teorema de convolución.  3.9 Transformada de una integral.  3.10 Transformada de una función periódica.  3.11 Transformada de la función delta de Dirac.  3.12 Aplicaciones.  Tema 4 Sistemas de ecuaciones diferenciales lineales. 4.1 Teoría preliminar.  4.1.1 Sistemas de ecuaciones diferenciales lineales.  4.1.2 Sistemas de ecuaciones diferenciales lineales homogéneos. 4.1.3 Solución general y solución particular de sistemas de ecua...
Leer más