Tema 3 Transformada de Laplace Jesus Daniel Ibarra Yepez
3.1.1 Definición de la transformada de LAPLACE
Las
transformadas de Laplace fueron formuladas para transformar una ecuación
diferencial que
contiene las
diferenciales de una función indefinida, a partir de una ecuación t-espaciada
hacia una ecuación
s-espaciada que puede ser resuelta con mucha facilidad.
También
pueden ser utilizadas para resolver un sistema de ecuaciones diferenciales.
Están
dirigidas a una amplia gama de problemas de valor inicial. La transformada de
Laplace
se denomina
a veces transformada operacional; esto es porque transforma las operaciones de
integración
en simples
operaciones algebraicas que son mucho más convenientes de resolver. Después de
la cual la
aplicación
de la técnica de la transformada inversa produce la solución exacta para la
ecuación diferencial dada.
3.1.2
Condiciones Suficientes De Existencia Para La Transformada De Laplace
Antes de
establecer las condiciones para la existencia de la transformada de Laplace
es esencial entender dos conceptos fundamentales
que constituyen la base de la transformada de Laplace.
Estos son: 1. Función continua a trozos: Se
dice que una función es a trozoso seccionalmente continua en un intervalo finito a <= t <= b si
el intervalo se puede subdividir en un número
finito de subintervalos, en cada uno de los cuales f(t) es continua y
tiene límites izquierdos, así como límites derechos.Considera una función f(t)
que es continua a trozos en [a, b], pero presenta discontinuidades en algunos
puntos.
3.2 Trasformada
Directa
Uno de los
algoritmos aritméticos más ampliamente utilizados es la transformada rápida de
Fourier, un medio eficaz de ejecutar un cálculo matemático básico y de
frecuente empleo.
La
transformada rápida de Fourier es de importancia fundamental en el análisis
matemático y ha sido objeto de numerosos estudios. La aparición de un algoritmo
eficaz para esta
operación
fue una piedra angular en la historia de la informática. Las aplicaciones de la
transformada rápida de Fourier son múltiples.
Es la base
de muchas operaciones fundamentales del procesamiento de señales, donde tiene
amplia utilización.
Además,
proporciona un medio oportuno para mejorar el rendimiento de los algoritmos
para un conjunto de problemas aritméticos comunes. Si la transformada de
Laplace de una función f(t) es F(s), esto es,
Entonces f(t) se denomina la transformada
inversa de Laplace de F(s) y se escribe como,
3.3
Transformada Inversa
Si la
transformada de Laplace de una función f(t) es F(s), esto es
Entonces
f(t) se denomina la transformada inversa de Laplace de F(s) y se escribe como,
Aquí L-1 es
llamado el operador de la transformada inversa de Laplace. Aunque existe una fórmula de inversión
compleja la cual proporciona un medio directo para determinar la transformada inversa
de Laplace de una función, esta implica un conocimiento amplio de la
integración compleja.
Sin embargo, no es posible encontrar una
transformada inversa de Laplace de todas las funciones por este camino.
Un punto interesante a destacar aquí es que la
transformada inversa de Laplace de una función puede no ser única.
Por ejemplo, sabemos que la transformada de
Laplace de f(t) = 1 es 1/ s
Sin embargo,
existe una función más para la que la transformada de Laplace resulta en el
mismo término, esta es, f(t) = 1 si 0 < t < 3 −8 si t = 3 1 si t > 3
Por lo
tanto, se puede concluir que la transformada inversa de Laplace de 1/s resulta
para dos funciones como se describe anteriormente. Sin embargo, entre las dos,
sólo f(t) = 1 es continua, por lo tanto, f(t) = 1 es la única función que tiene
la transformada de Laplace como 1/ s. También es posible escribir una
transformada inversa de Laplace en la forma de integración, la cual es llamada
integral de Fourier Millen o integral Bromwich o fórmula inversa de Millen. Se
trata de una integral de línea y es denotada como.}
3.4 FUNCIÓN
ESCALÓN UNITARIO.
3.5 Teoremas
de traslación
Cuando necesitemos encontrar
la transforma de laplace del producto de la función exponencial e^at por una
función f(t), sin usar la definición, podemos decir que la transformada es
igual F(s-a) donde F(s) es la transformada de laplace de f(t) y F(s-a) implica
sustituir por s a s-a en la tranformada F(s). A esto se le conoce como el
primer teorema de traslación de la transformada de laplace, el cual en este
video no solo mostramos como usarlo sino que también demostramos porque es
cierto.
Cuando tengamos que hallar la transformada de
Laplace de una función exponencial que multiplica a una función cualquiera
f(t), vamos a decir que esta transformada es igual a transformar a f(t) de la
siguiente manera: F(s)=L[f(t)] y sustituir a s en F(s) por s-a, matemáticamente
estas palabras se expresan como L[(e^at)f(t)]=F(s-a) con F(s)= L[f(t)], esta
manera de escribir la transformada de Laplace se conoce como el primer teorema
de translación , otra forma de ver esto es: L[(e^at)f(t)]= L[f(t)]s→s-a.
Veamos un ejemplo para que entendamos mejor como
aplicar estas definiciones, supongamos entonces que nos piden hallar la
transformada de Laplace para la siguiente función: L[(e^2t)(t^3)], entonces lo
que nos dice el teorema es que debemos hallar la transformada de f(t) que en
este caso es t^3 y luego reemplazar a s por s-a. En videos anteriores habíamos
visto que la transformada de t^3 se puede hallar usando tablas de transformadas
de Laplace que existen para funciones comunes tales como esta, vemos entonces
que la transformada de Laplace para esta función es igual a: L[t^3]=3!/s^4,
luego lo que nos dice el teorema es que cambiemos a s por s-a, realizando este
procedimiento, tenemos entonces la transformada de Laplace para el problema que
nos pidieron resolver es: L[(e^2t)(t^3)]= 3!/(s-2)^4, teniendo en cuenta que a
es el coeficiente que acompaña a la t y que en este caso es dos.
Observemos que este teorema nos permite ahorrar
mucho tiempo ya que nos evita tener que usar la definición de la transformada
de Laplace. En el video se muestra otro ejemplo de más complejidad y se muestra
de manera detallada la demostración del teorema de translación a partir de la
definición de transformada de Laplace vista en los videos anteriores.
3.6Transformada
de funciones multiplicadas por tn, y divididas entre t
En este
subtema y los siguientes se desarrollarán varias propiedades operacionales de
la transformada de Laplace. En particular, se verá como hallar la transformada
de una función f(t) que se multiplica por un monomio tn, la transformada de un
tipo especial de integral y la transformada de una función periódica. Las dos
últimas propiedades de transformada permiten resolver ecuaciones que no se han
encontrado hasta este momento: ecuaciones integrales de Volterra, ecuaciones
integro diferenciales y ecuaciones diferenciales ordinarias en las que la
función de entrada es una función periódica definida por partes.
Transformada de derivadas (teorema)
Al igual que
en una función ordinaria, la transformada de Laplace también puede aplicarse al
diferencial de una función. En tal situación, colocamos en la fórmula el
diferencial de la función en el lugar de la función real para derivar la
transformada de Laplace, que es,
Transformada
de integrales (teorema) Hasta ahora hemos estudiado la forma de determinar la
transformada de Laplace de una función dada.
Pero, como sabemos, existen varias operaciones que pueden realizarse en
una determinada función. Una de las
principales operaciones entre ellas es la integración. Como sabemos, la
integración de una función nos da otra función. Por lo tanto, es esencial saber
si la técnica de la transformada de Laplace puede aplicarse a la integral de
una función real.
La respuesta
a la pregunta anterior es afirmativa, hasta cierto punto.
La cláusula
de “hasta cierto punto”, se añade aquí porque esto no es cierto para todas las
integrales.
Existen
ciertos pre-requisitos que deben ser verdaderos para obtener la transformada de
Laplace de la integral de la función real.
La función
real debe estar definida para la variable de tiempot, también la función debe
ser definida de forma continua en el intervalo [0, ).
3.7 transforma
dada de una derivada y derivada de una transformada
En este caso, sabemos que la función (t)
toma el valor de cero para todos los valores de t, excepto en t = 0. Esto
implica que el valor de la función f(t) también se vuelve insignificante, excepto
cuando el argumento tde la función se convierte en cero.
En tal
situación, tenemos el valor del integrando f(0) (t), f(0)que puede tomarse
fuera dado que se convierte en una constante, haciéndolo de esta manera
obtenemos el lado derecho de la ecuación. Por lo tanto, podemos pensar en (t)
dt como el operador funcional que saca el valor de la función cuando el
argumento de la función es igual a cero. Otra forma popular de definir una
función delta de Dirac es una medida, ya que la función delta de Dirac tiene
como su argumento un subconjunto de los números realesS, es decir, S R. Aquí,
el valor de S es cero cuando la salida de la función es uno o infinita y en
otro caso, el subconjunto S puede tomar elementosinfinitos:
Veamos ahora un ejemplo de la función delta de
Dirac.
Resuelve y’
+ 2y’ – 15y = 6 (t – 9) dados y(0) = −5 ey’(0) = 7
Aplicando la
transformada de Laplace para la función dada obtenemos: s2Y(s) – sy(0) – y’(0)
+ 2(sY(s) – y(0)) – 15Y(s) = 6e-9s = (s2 + 2s – 15)Y(s) + 5s + 3 = 6e-9s
Resolviendo
la ecuación anterior obtenemos, Y(s) = 6e-9s F(s) – G(s) Ahora haciendo uso de
las fracciones parciales para obtener la transformada inversa de Laplace como,
F(s) = 1/ [(s + 5) (s – 3)] = [(1/ 8)/ (s – 3)] – [(1/
8)/ (s + 5)] f(t) =
(1/8) e3t - (1/8)e-5t
G(s) = [5s + 3/(s + 5) (s – 3)] = [(9/4)/ (s – 3)] + [(11/4)/ (s + 5)] f(t) =
(9/4) e3t - (11/4)e-5t
Por lo
tanto, la solución es Y(s) = 6e-9s F(s) – G(s):
Esto implica
que la función delta de Dirac no es una función real sino que es una distribución
que se extiende por un intervalo definido para la función dada. También es
llamada una función singular. Como tal, no existe una definición formal de esta
función. Pero puede ser definida mediante utilizar la propiedad de la propia
función, la cual es,
En términos
simples, podemos decir que una función delta de Dirac es aquella cuya salida se
calcula a cero para cada valor del argumento de entrada, excepto cuando el
valor del argumento de la función en sí es igual a cero.
Aquí el argumento de la función es un
parámetro valorado real. La integral de la función en el rango de parámetros (-
, ) es uno.
A la luz de
la afirmación anterior, podemos concluir que esta es una función real desde el
punto de vista matemático, ya que para cualquier función real cuyo valor es
constante, excepto en un punto, el valor de la integral debe calcularse a cero,
el cual no es este caso.
La gráfica
de la función se vería algo así como:
En términos
simples, podemos decir que una función delta de Dirac es aquella cuya salida se
calcula a cero para cada valor del argumento de entrada, excepto cuando el
valor del argumento de la función en sí es igual a cero. Aquí el argumento de
la función es un parámetro valorado real. La integral de la función en el rango
de parámetros (- , ) es uno.
A la luz de
la afirmación anterior, podemos concluir que esta es una función real desde el
punto de vista matemático, ya que para cualquier función real cuyo valor es
constante, excepto en un punto, el valor de la integral debe calcularse a cero,
el cual no es este caso. La gráfica de la función se vería algo así como:
En este
caso, sabemos que la función (t) toma el valor de cero para todos los valores
de t, excepto en t = 0.
Esto implica
que el valor de la función f(t) también se vuelve insignificante, excepto
cuando el argumento tde la función se convierte en cero. En tal situación,
tenemos el valor del integrando f(0) (t), f(0)
que puede
tomarse fuera dado que se convierte en una constante, haciéndolo de esta manera
obtenemos el lado derecho de la ecuación.
Por lo
tanto, podemos pensar en (t) dt como el operador funcional que saca el valor de
la función cuando el argumento de la función es igual a cero.
Otra forma popular de definir una función
delta de Dirac es una medida, ya que la función delta de Dirac tiene como su
argumento un subconjunto de los números realesS, es decir, S R.
Aquí, el
valor de S es cero cuando la salida de la función es uno o infinita y en otro
caso, el subconjunto S puede tomar elementosinfinitos. Veamos ahora un ejemplo
de la función delta de Dirac.
Resuelve y’
+ 2y’ – 15y = 6 (t – 9) dados y(0) = −5 ey’(0) = 7 Aplicando la transformada de
Laplace para la función dada obtenemos,
s2Y(s) – sy(0) – y’(0) + 2(sY(s) – y(0)) – 15Y(s) =
6e-9s = (s2 + 2s – 15)Y(s) + 5s + 3 = 6e-9s
Resolviendo
la ecuación anterior obtenemos, Y(s) = 6e-9s F(s) – G(s) Ahora haciendo uso de
las fracciones parciales para obtener transformada inversa de Laplace como,
F(s) = 1/ [(s + 5) (s – 3)] = [(1/ 8)/ (s – 3)] – [(1/
8)/ (s + 5)] f(t) = (1/8) e3t - (1/8)e-5t G(s) = [5s + 3/(s + 5) (s – 3)] =
[(9/4)/ (s – 3)] + [(11/4)/ (s + 5)] f(t) = (9/4) e3t - (11/4)e-5t
Por lo
tanto, la solución es Y(s) = 6e-9s F(s) – G(s)
3.8 TEOREMA
DE CONVOLUACIÓN.
Si L-1{F(s)}
= f(t) y L-1{G(s)} = g(t)entonces
Entonces
obtenemos, L{ f(u) g(t – u) du} = e-stf(u) g(t – u) du dt = f(u) { e-st g(t –
u) dt} du=
fijando t – u = v obtenemos, dt = dv = f(u) {
e-s(u + v) g(v) dv} du = { e-suf(u) du}. e-sv g(v) dv} O, L{ f(u) g(t – u) du}
= F(s) G(s)
Invirtiendo
ambos lados de la ecuación obtenemos, L-1{F(s) G(s)} = f(u) g(t – u) du
L-1{F(s) G(s)} = f * g
Existe una
cantidad amplia de problemas que pueden resolverse con la ayuda del teorema de
convolución.
Uno de estos
problemas se da aquí para hacer el concepto más claro. Usa el teorema de
convolución para determinar L-1{1/ [s2 (s + 1)2]}
Sea F(s) =
1/ s2 Y G(s) = 1/ (s + 1)2entonces, f(t) = L-1{F(s)} = L-1(1/ s2) = t g(t) =
L-1{G(s)} = L-1(1/ (s + 1)2) = e-t L-1(1/ s2) = t e-t Por lo tanto, con la ayuda del teorema de
convoluciónpodemos escribir,
L-1{1/ [s2 (s + 1)2]} = f(u) g(t – u) du = u
(t – u) e-(t – u) du = e-t [t u eudu - u2eu du] = e-t [t (u eu – eu) - (u2eu) +
2 u eu du] = e-t [t {(t – 1) et + 1} – t2 et + 2(ueu – eu) ]
= e-t [t (t – 1) et + t + t2 et + 2(tet – et +
1)] = e-t [t2 et - tet+ t - t2 et + 2tet - 2et + 2] = e-t [tet+ t- 2et + 2] = t
+ tet– 2 + 2et
El teorema
de convolución tiene amplias aplicaciones en la práctica. También se utiliza en
la teoría de circuitos para calcular la respuesta al impulso de un circuito
concreto.
Aquí x(t) es la entrada del sistema, y(t) es
la salida del sistema y h(t) es la respuesta al impulso del sistema. Por
consiguiente, la salida del sistema calculado con la ayuda de la operación de
convolución está dada por, y(t) = x(t) * h(t)
Aquí la
función anterior está en el dominio de t, por lo tanto, los cálculos pueden ser
algo crípticos, por esto, con el propósito de conveniencia en los cálculos,
esta puede ser transformada en el dominio s. La operación de convolución en el
dominio s se convierte en la operación de multiplicación. L{a(t) * b(t)} = A(s)
B(s)
3.9
TRANSFORMADA DE UNA INTEGRAL.
Hasta ahora
hemos estudiado la forma de determinar la transformada de Laplace de una
función dada. Pero, como sabemos, existen varias operaciones que pueden
realizarse en una determinada función. Una de las principales operaciones entre
ellas es la integración. Como sabemos, la integración de una función nos da
otra función. Por lo tanto, es esencial saber si la técnica de la transformada
de Laplacepuede aplicarse a la integral de una función real. La respuesta a la
pregunta anterior es afirmativa, hasta cierto punto. La cláusula de “hasta
cierto punto”, se añade aquí porque esto no es cierto para todas las
integrales. Existen ciertos pre-requisitos que deben ser verdaderos para
obtener la transformada de Laplace de la integral de la función real. La función
real debe estar definida para la variable de tiempot, también la función debe
ser definida de forma continua en el intervalo [0, ). Asimismo, el integral de
esta función debe ser una función continua a trozos para el mismo intervalo,
esto es, [0, ). Y, por último, ambas, la función real como el diferencial de la
función real deben ser de orden exponencial cuando el valor de t tiende al
infinito. Esto significa que deben existir dos números reales positivos M y ,
un número T tal que,
3.10 TRANSFORMADA
DE UNA FUNCIÓN PERIÓDICA.
Aquí el
valor de t debe ser siempre mayor o igual que T. Asumiendo que las condiciones anteriores son válidas para
la función de entrada y L{f(t)} = F(s), entonces la transformada de Laplace de
la integral de la función real puede darse como,
Aquí el valor de t debe ser siempre mayor o igual que T. Asumiendo que las condiciones anteriores son válidas para la función de entrada y L{f(t)} = F(s), entonces la transformada de Laplace de la integral de la función real puede darse como,
Esto puede reorganizarse como,
En términos
simples, podemos decir que para la función periódica f(t) conperíodo a, la
transformada de Laplace es equivalente a la transformada de Laplace en un
período
único de
esafunción dividida por el término (1 - e-as). También existe una prueba del
teorema indicado arriba. Dado que f(t) es una función periódica con período a,
f(t + a) = f(t), f(t + 2a) = f(t) y así sucesivamente. Ahora,
L{f(t)} = e-st f(t) dt = e-stf(t) dt + e-st f(t) dt + e-st f(t) dt + … Estableciendo t = (u + a) en la
segunda integral, t = (u + 2a) en el tercer integral etc. Entonces obtenemos, =
e-stf(t) dt + e-s(u + a) f(u + a) du + e-s(u + 2a) f(u + 2a) du + … = e-suf(u)
du + e-su f(u + a) du + e-2sa e-su f(u) du + … = (1 + e-as + e-2as+ …) e-su
f(u) du = (1 - e-as)−1 e-stf(t) dt [Dado que 1 + x + x2 + … = (1 – x)−1]
L{f(t)} = [1/ (1 - e-as)] e-st f(t) dt Por consiguiente, podemos ver que para
llevar a cabo la operación de transformación de Laplace a una función periódica
necesitamos romper esa función en los sub-intervalos, lo cual depende de los
intervalos para los cuales la función dada está definida. La sumatoria de todas las integrales
produce la transformada de Laplace para esa función. Sin embargo, es posible
aplicar directamente el teorema discutido anteriormente con propósitos de
conveniencia para la solución de problemas. Se provee un ejemplo ilustrando el
uso de este teorema para hacer más claro los conceptos.
Muestra que
si f(t + a) = -f(t), entonces, L{f(t)} = [1/ (1 + e-as)] e-st f(t) dt Dado
quef(t + 2a) = f[(t + a) + a)] = -f(t + a) = -[-f(t)] = f(t) La función f(t)
dada es una función periódica con período 2a. Ahora, utilizando el teorema para
la transformada de Laplace de funciones periódicas con el período a reemplazado
por 2a tenemos que, L{f(t)} = [1/ (1 - e-2as)] e-st f(t) dt = [1/ (1 - e-2as)]
[ e-stf(t) dt + e-st f(t) dt]
Estableciendo t = (u + a) en la segunda integral, tenemos que L{f(t)} =
[1/ (1 - e-2as)] [ e-st f(t) dt + e-s(u + a) f(u + a) du] = [1/ (1 - e-2as)] [
e-stf(t) dt – e-as e-su f(u) du] = [(1 - e-as)/ (1 - e-2as)] e-stf(t) dt
L{f(t)} = [1/ (1 + e-as)] e-st f(t) dt
3.11transformada
de Laplace de la función delta Dira
Una función
delta de Dirac es una función especial cuyo valor es cero en todos los puntos,
excepto en un punto, este es cuando el argumento de la función es igual a cero.
Esto se denota como,
Cambiemos la
función delta de Dirac por una constante, digamos c.
Entonces
ahora la definición de esta función delta de Dirac desplazada es, (t – c) = 0,
t <> c = , t = c Esto es sólo una pseudo definición de la función. Ahora
bien, si derivamos el área de la función para los límites de integración (- ,
), y resulta ser uno, esto es, (t – c) dt = 1 Se trata de una derivación importante
y esta también nos da la noción de pseudo infinidad ,como en la definición
función deltade Dirac desplazada. Aquí, la palabra pseudo se utiliza ya que
pueden existir diferentes medidas del infinito mediante tomar un producto del
infinito con un número entero. Para entenderlo, integremos el producto de la
función delta de Dirac y un entero, digamos dos para los mismos límites de
integración, esto es, (- , ). 2 (t – c) dt Uno podría suponer que la salida de
la integración debería ser igual a dos, ya que, = 2 (t – c) dt = (2) (1) = 2 Es
decir, si la función delta de Dirac se multiplica por dos, el infinito sería
dos veces más grande que antes. Ahora, multiplicando la función delta de Dirac
desplazada por alguna otra función, digamos f(t) y tomando la transformada de
Laplace de esta, es decir, L{ (t – c) f(t)} En el caso de que uno desee
determinar únicamente la transformada de Laplace de la función delta de Dirac
desplazada, asumimos que el valor de f(t) es uno. Esto es, tenemos, e-st f(t)
(t – c) dt Como sabemos, el proceso de
integración nos da el área de la función que está siendo integrada. Por lo
tanto, primero dibujemos el área de las dos funciones para averiguar qué área
estamos determinando realmente. Mientras lo hacemos, asume que f(t) es
arbitrario. Por tanto, tenemos el gráfico de la función como,
Iginio Soto.
(2015). Ecuaciones Diferenciales. Cd.Victoria: Itcv.
DocPlayer. (2019).
EcuacionesDiferenciales. 30/06/22, de DocPlayer Sitio web:
https://ocplayer.es/98162073-Ejercicios-resueltos-de-transformada-directa-de-laplace.html
Guillermo
Vivaldo Vázquez. (2015). 2015 . 30/06/22, de googleSite Sitio web:
https://sites.google.com/site/ecuacionesdiferenciales2015/parcial-2



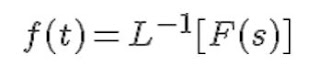







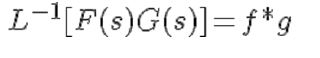









Comentarios
Publicar un comentario