Tema 4 Sistemas de ecuaciones diferenciales lineales Jose Eduardo Guerrero Islas
4.1.1 Sistemas de EDL
Los problemas de la vida real pueden representarse
de mejor manera con la ayuda de múltiples variables. Por ejemplo, piensa en el
conteo de la población representado con la ayuda de una sola variable. Pero,
esta depende del conteo de la población de depredadores así como también de las
condiciones climáticas y la disponibilidad de alimentos. Todas estas
condiciones en sí mismas forman una ecuación diferente definida en una variable
separada. Por lo tanto, para estudiar las relaciones complejas, requerimos de
varias ecuaciones diferentes para definir diferentes variables. Tal sistema es
el sistema de ecuaciones diferenciales. Un sistema de ecuaciones diferenciales
lineales se puede denotar como:
Aquí xi (t) es una variable en términos de tiempo y el valor
de i = 1, 2, 3, …, n. También A es una matriz que contiene todos los términos
constantes, como [ai,j]. Dado que los coeficientes de la matriz constante A no
están definidos explícitamente en términos de tiempo, por lo tanto, un sistema
de ecuaciones diferenciales lineales es llamado a veces autónomo.
La notación convencional general para el sistema de
ecuaciones diferenciales lineales es:
dx/ dt = f(t, x, y) dy/ dt = g(t, x, y)
El sistema anterior de ecuaciones diferenciales tendrá
numerosas funciones para satisfacerla. Mediante la modificación de la variable
tiempo obtendremos un conjunto de puntos que se encuentran en el plano de dos
dimensiones x-y, los cuales se denominan trayectoria. La velocidad con respecto
a esta trayectoria, en algún tiempo t es, = (dx/ dt, dy/ dt).
Un ejemplo de un sistema de ecuaciones diferenciales
lineales es el siguiente:
dx1/ dt = −4×1 + 2×2
dx2/ dt = 0×1 + −2×2
Con el fin de determinar el conjunto completo de fórmulas
para la variable dependiente de tiempo xi(t) para todos los valores de i, es
necesario obtener primero los vectores propios y valores propios de la matriz
constante A. En el caso que la matriz constante A posea un conjunto de valores
propios repetidos para sus componentes, sería necesarioun vector propio generalizado.
Este es t, toma en cuenta que los vectores propios y valores propios de la
matriz constante puede ser un subconjunto de los números reales o también un
subconjunto de los números complejos.
La representación de la matriz del problema anterior es la siguiente, dx/ dt = A * x En este caso, A es la matriz constante que puede ser representada como:
Y x(t)T es un vector de variables definidas en términos de
tiempo, el cual es representado como:
En caso de que el vector propio de la matriz constante A sea
un subconjunto de los números reales para este ejemplo, podemos escribir:
A = S * D * S-1
Aquí D es la matriz diagonal de la matriz de vectores
propios de la matriz constante A y S es la matriz que contiene los vectores
propios en forma de columnas, en el mismo orden como los valores propios se
escriben en la matriz diagonal D. En consecuencia, la forma de la matriz del
ejemplo anterior se puede escribir como:
dx/
dt = A * x
dx1/ dt dx2/
dt = −4 2
0 −4 * x1 x2
4.1.2 Sistemas de EDL homogéneos
Sabemos que una ecuación diferencial lineal es de la
forma:
Si esta misma ecuación se transforma en la forma, obtenemos una ecuación diferencial lineal homogénea.
Esta se da cuando una gran cantidad de tales ecuaciones juntas, de manera tal que dependen unas de las otras, y definen colectivamente un problema común, entonces se les llama un sistema de ecuaciones diferenciales lineales homogéneas. Tales sistemas pueden ser resueltos de manera eficiente con la ayuda de las matrices, las cuales son denominadas matriz fundamental. Sean X1, X2… X3 las soluciones de la matriz fundamental del sistema de entrada de ecuaciones diferenciales homogéneas, entonces puede representarse de manera condensada como:
En la ecuación anterior, las soluciones del sistema
de ecuaciones diferenciales están definidas en algún intervalo, digamos I y la
solución general del sistema de ecuaciones diferenciales es este:
En la ecuación anterior, los términos que se mantienen
dentro de los corchetes son los vectores fila, donde X1 = [xi1j], X2 =
[xi2j]…Xn = [xinj]. Estas son las soluciones n fundamentales del sistema de
entrada de ecuaciones diferenciales lineales homogéneas para el intervalo dado
I. Entonces tenemos que la matriz fundamental para el sistema homogéneo de
ecuaciones diferenciales lineales para el intervalo dado como I es:
Ejemplo:
Ahora la matriz del sistema es escalonada, y el
número de los renglones no nulos es r = 3 = n. Por eso el sistema es compatible
determinado, esto es, la única solución
es la trivial: x = 0. En este ejemplo no hay sentido hacer la comprobación para
x = 0. Seria más importante comprobar que la matriz del sistema en forma
escalonada efectivamente tiene 3 renglones no nulos (en otras palabras, que el
rango del sistema es igual a 3), pero en este momento del curso no tenemos
métodos para comprobarlo.
4.1.3 Solución general y solución particular de sistemas de
ecuaciones diferenciales lineales. ECUACIONES
DIFERENCIALES SEPARABLES
Una ecuación en la que aparecen x,y, y´y´´,... y
y(n) , donde y es una función de x y y (n) es la nesima derivada de y con
respecto a x, es una ecuación diferencial ordinaria de orden n. Los siguientes
ejemplos son ecuaciones ordinarias del orden especificado:
ORDEN 1: Y´=2x
ORDEN 2: D²y / dx² + x²( dy / dx )³ - 15y= 0
ORDEN 3: ( y¨¨)4 – x²(y¨ )5 + 4xy = x ex
ORDEN 4: (d 4y /dx4 ) - 1 = x³ dy/ dx
Recordemos que una función f (o f(x) es una solución
de una ecuación diferencial si al sustituir y por f (x) se obtiene una
identidad para todo x en un intervalo. Por ejemplo, la ecuación diferencial Y´
= 6x 2 - 5
Tiene solución
F (x) = 2x3 - 5x + C
Para todo real C, porque al sustituir y por f(x) se
llega a la identidad 6x 2 - 5 = 6x 2 - 5. Se dice que f(x) = 2x 3 - 5x + C es
la solución general de y´= 6x 2 - 5 porque todas las soluciones son de esta
forma. Se obtiene una solución particular asignando valores específicos a C.
Por ejemplo, tomando C = 0 se obtiene la solución particular y = 2x3 – 5x. A
veces se dan condiciones iniciales para determinar una solución particular,
como se ilustra en el siguiente ejemplo
Ejemplo
1. Encontrar
la solución general de la ecuación diferencial y´= 2x
2. Obtener
una solución particular de y´ = 2x que satisfaga la siguiente condición: y = 3
cuando x = 0
SOLUCIÓN
3. Si
f es una solución de y´ = 2x, entonces f´´(x) = 2x. La integral indefinida
lleva a la solución general Y = f (x) = x² + C.
Podemos encontrar soluciones particulares asignando
valores específicos a C. Así obtenemos la familia de parábolas y = x² + C
4. Si
y = 3 cuando x = 0, entonces sustituyendo en y = x² + C obtenemos 3 = 0 + C, o
bien C = 3. Por lo tanto, la solución particular es y = x² + 3
4.2 Métodos de solución para sistemas de
ecuaciones diferenciales lineales
Un sistema de diferenciales lineales puede resolver
las ecuaciones. Al igual que existen varias técnicas para resolver una ecuación
diferencial lineal, también las hay para un sistema de ecuaciones diferenciales
lineales. Como el método de eliminación de gauss, método separable etc. Sea un
sistema de ecuaciones diferenciales lineales representado como:
Entonces la representación de la matriz equivalente
de este sistema de ecuaciones diferenciales lineales será.
4.3 Método de los operadores
Laplace
Cuando se especifican las condiciones iniciales, la
transformada de Laplace reduce un sistema de ecuaciones diferenciales lineales
con coeficientes constantes aun conjunto de ecuaciones algebraicas para las
funciones transformadas.
La ventaja que tiene el método de transformada de
Laplace sobre estos métodos ordinarios, es que ésta:
Ejemplo De Laplace
Entonces tenemos que S=3 S=2 B=1 A=-1 por lo tanto
Método De Solución Por Operadores
Operadores diferenciales En cálculo, la
diferenciación suele indicarse con la D mayúscula; esto es dy/dx=Dy.
El símbolo D se llama operador diferencial porque
transforma una función diferenciable en otra función; por ejemplo:
Las derivadas de orden superior se pueden expresar
en términos de D en forma natural:
En donde y representa una función suficientemente
diferenciable. Las expresiones poligonales donde interviene D, como:
También son operadores diferenciales. En general, el
operador diferencial de orden n se define:
Como consecuencia de dos propiedades básicas de la
diferenciación, D(cf(x))=cDf(x) donde c es una constante y
D{f(x)+g(x)}=Df(x)+Dg(x), el operador diferencial L tiene una propiedad de
linealidad; es decir, L, operando sobre una combinación lineal de dos funciones
diferenciables, es lo mismo que una combinación lineal de L operando sobre las
funciones individuales. En símbolos, esto significa que:
En donde Q y ,B son constantes. A causa de la
propiedad (9), se dice que el operador diferencial de orden n, L, es un
operador lineal. Ecuaciones diferenciales Toda ecuación diferencial lineal se
puede expresar en notación D; por ejemplo, la ecuación diferencial
se puede escribir en la forma
Como
Al aplicar la ecuación (8), las ecuaciones
diferenciales (6) y (7) de orden n se pueden escribir en forma compacta como:
4.4 Utilizando la transformada de Laplace
La Transformada de Laplace es una técnica Matemática
que forma parte de ciertas transformadas integrales como la transformada de
Fourier, la transformada de Hilbert, y la transformada de Mellin entre otras.
Así se identifica
Estas transformadas están definidas por medio de una
integral impropia y cambian una función en una variable de entrada en otra
función en otra variable. La transformada de Laplace puede ser usada para
resolver Ecuaciones Diferenciales Lineales y Ecuaciones Integrales. Aunque se pueden
resolver algún tipo de ED con coeficientes variables, en general se aplica a
problemas con coeficientes constantes.
Cuando se resuelven ED usando la técnica de la
transformada, se cambia una ecuación diferencial en un problema algebraico.
Pierre- Simon Laplace La metodología consiste en aplicar la transformada a la
ED y posteriormente usar las propiedades de la transformada. El problema de
ahora consiste en encontrar una función en la variable independiente tenga una
cierta expresión como transformada.
¿EN
QUE SE UTILIZA?
El Método de la transformada de Laplace es un método
operacional que puede usarse para resolver ecuaciones diferenciales lineales.
Con el uso de la transformada de Laplace muchas funciones sinusoidales y
exponenciales, se pueden convertir en funciones algebraicas de una variable
compleja s, y reemplazar operaciones como la diferenciación y la integración,
por operaciones algebraicas en el plano complejo.
4.5 Aplicaciones
Existen varias aplicaciones donde se le pueden dar
uso de las ecuaciones diferenciales lineales, como por ejemplo para la
resolución de algunos problemas físicos. Muchos de ellos se rigen por
ecuaciones lineales. Este es el caso de los circuitos eléctricos para el
cálculo de la corriente y de la tensión en cada uno de los elementos del
circuito, y de los sistemas mecánicos elásticos de los que se quieren estudiar
sus vibraciones. También pueden aparecer ecuaciones lineales en algunos
problemas de movimiento, como aquellos en los que el móvil sigue una
trayectoria rectilínea. Ejemplo


.jpeg)





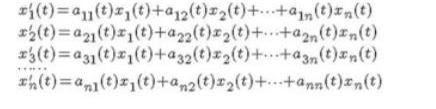















Comentarios
Publicar un comentario